Crypto

Category: crypto
Difficulty: easy
Author: KPMG
Tags: Diffie–Hellman, Public Key
Description:

Alice: Hey, I managed to get another flag from H@ckademy.
Bob: Oh, please send it over.
Alice: Sure, but just in case, I'll encrypt it—who knows who might be listening.
Bob: Ok.
Alice: Let's use our reliable script for secret exchange. You know, the Diffie-Hellman one.
Bob: Ah, our first project in Python.
Alice: Alright, I'm sending the data:
g=577
p=10332921861938291919377635159012636040519117927041835671194203494937679183911345052843111512544303969800681115505917911462916407940308340306260755239268943
A=8370337962458643162004582468469045984889816058567658904788530882468973454873284491037710219222503893094363658486261941098330951794393018216763327572119677
Bob:
B=9755909033513767641159594933585734179714892615169429957597029280980531443144704341694474385957669949989090202320232433789032328934018623049865998847328154
Alice: Here’s the encrypted flag. UYaG0KR+k8SmDn9ag/LV9u8h76iXpy6n5D7u00Y3rU/+suuGWSvm6J1ajXO2HxGgt6gyDFtNUZnsgfxGBAysGg==
Bob: Thanks a lot. Thanks to our flawless Diffie-Hellman implementation, there's no way anyone could decrypt it, hehe.

Handout files

DH_shared_secret_generation

Get Familiar with the Task

I assume you've already read the description and noticed that the flag in this challenge resembles a familiar Base64 encoding. However, after decoding it, you see what looks like a series of random bits:

Q††Ð¤~“ĦZƒòÕöï!益§.§ä>îÓF7­Oþ²ë†Y+æèZs¶ ·¨2 [MQ™ìüF ¬

This time, the flag was truly encrypted. In this challenge, the hint is hidden in the description, so you need to understand how the Diffie–Hellman key exchange algorithm works and identify the flaw in this flawless implementation.

You can familiarize yourself with this key exchange method by reading my previous post, or you can move on to the next part if you already know how it works.

At first glance, the code may seem correct. It has separate and clean functions for generating public keys, shared keys, and for encrypting and decrypting messages. So, let's test this app with our arbitrary values.

Let's test with \( p = 23 \), \( g = 9 \), and \( ext{priv\_ka} = 4 \).

That's an unexpected value for Alice's public key.

According to the calculation:

$$ 9^4 \bmod{23} = 6 $$

Not 13, as shown in the screenshot. So why does this unexpected value occur, and where does it come from? Let's take a closer look at what exactly happens between receiving the input values and generating the public key.

def generate_public_int(g, a, p):
    return g ^ a % p


def generate_shared_secret(A, b, p):
    return A ^ b % p

You may have already spotted the mistake, but if not, let me explain.
The correct formula for key generation is:

$$ g^{\text{priv_ka}} \bmod{p} $$

The code looks similar, but it doesn't work that way! In Python, the ^ symbol represents the bitwise XOR operation, not exponentiation!

Therefore, in pseudocode:

g^a = g XOR a

What does this mean for us? The operation here is performing an exclusive OR (XOR). If you're not familiar with this function, check out the Wikipedia article. Now, let's look at the bit values:

00000100 = 4
00001001 = 9
_____________
00001101 = 13

Once we've found the mistake, we can start recovering the key. Since the length of Alice's public key is shorter than Prime \( p \), the modulo operation has no effect on it. That means:

g ^ A \( \bmod{p} \equiv \) g ^ A

And since XOR is reversible and we have \( A \), which was produced by the equation g^A, by performing the XOR operation once again, we will recover Alice's private secret. You can perform this on your own, but here's the result:

Alice's Key

8370337962458643162004582468469045984889816058567658904788530882468973454873284491037710219222503893094363658486261941098330951794393018216763327572120124

Then, simply paste all data into the original program without any modifications required.

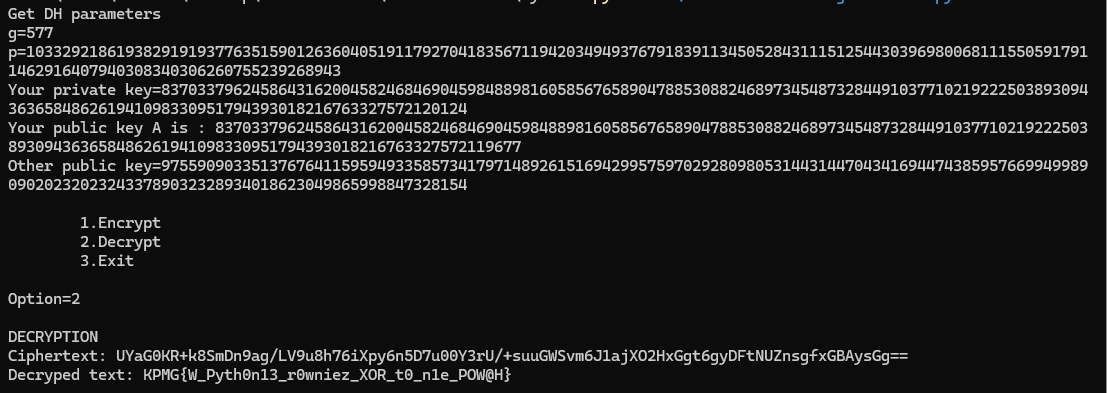
Here is the flag:

KPMG{W_Pyth0n13_r0wniez_XOR_t0_n1e_POW@H}